Causality in GANs

This semester I'm taking a course at UMBC called Causality in Machine Learning by Dr. Osman Gani. So far, we've studied Simpson's Paradox, Causality and the Potential Outcomes Framework, Average Treatment Effect, Ignorability, Exchangability, Identifiability, Consistency, Structural Causal Models (i.e. Local Markov Assumption, Forks, Colliders, Chains), Interventions, d-separation, and the Adjustment Formula. One part of my course grade is completing a class project. As a result, this has led me to research the concept of causality applied to generative adversarial networks. Here, I share some of my notes and observations on two papers I found interesting, CausalGAN and Counterfactual Generative Models. The overall goal of incorporating causality, primarily learning a structural causal model, in GANs is to produce images that are more creative than what can be learned from the original training data. One can control the generation of specific factors, like mustaches on women, as well as generate very diverse images that improve the training of a more robust, invariant image classifier.
CausalGAN
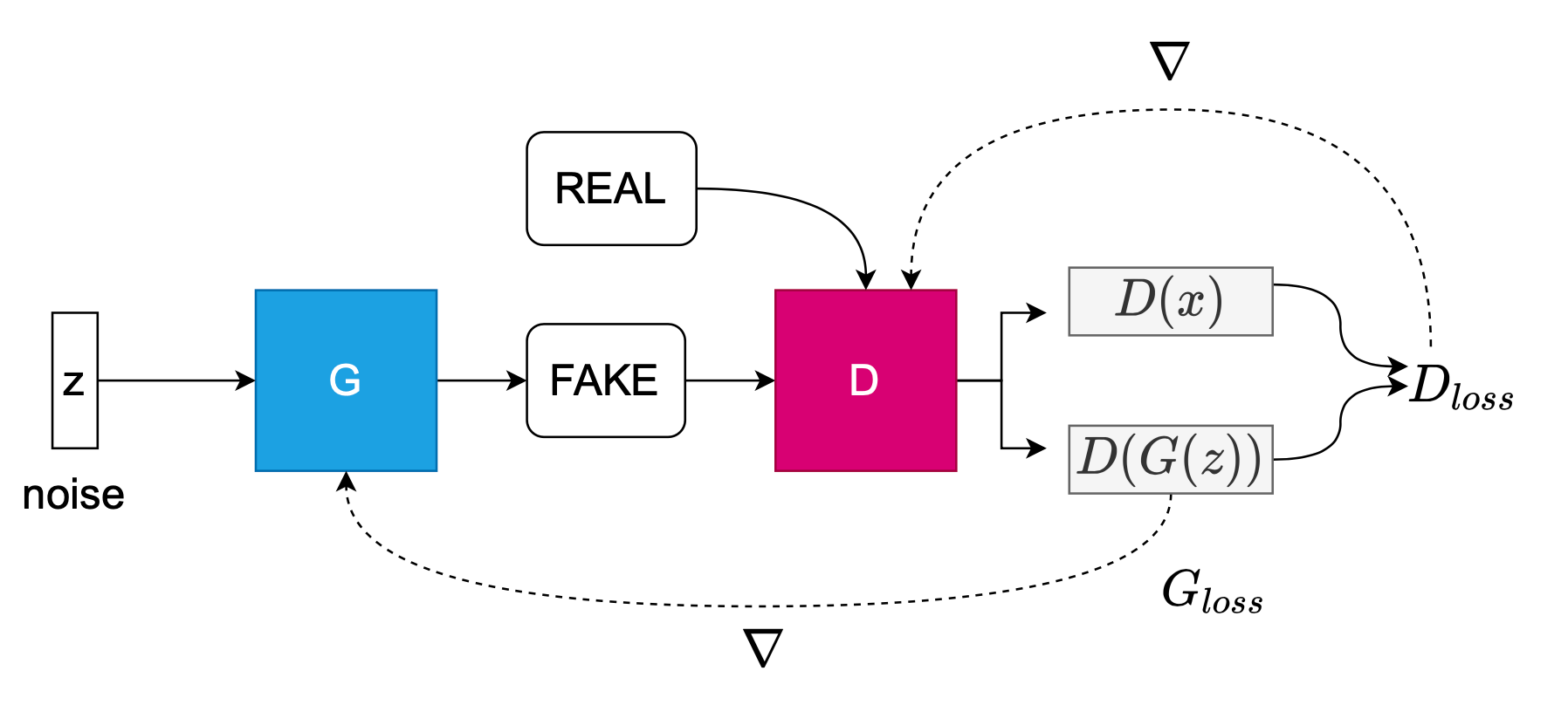
Both CausalGAN and Counterfactual Generative Models (CGM) actively use class labels as a conditioning source of side information into their generative models. As such, it is important to briefly describe a Conditional GAN. Conditioning the generator on an image given a label, \(p(D(G(z|y)))\), is a commonly used approach in GANs to regularize and introduce side information. Compare the conditional GAN objective (first equation) to the Vanilla GAN objective described by Goodfellow et al. (second equation).
\[\min\limits_{G}\max\limits_{D} V(D,G) = E_{x \sim p_{data}(x)} \log D(x|y) + E_{z \sim p_z(z)} \log (1 - D(G(z|y))\]
\[\min\limits_{G}\max\limits_{D} V(D,G) = E_{x\sim p_{data}(x)} \log D(x) + E_{z \sim p_z(z)} \log (1 - D(G(z))\]
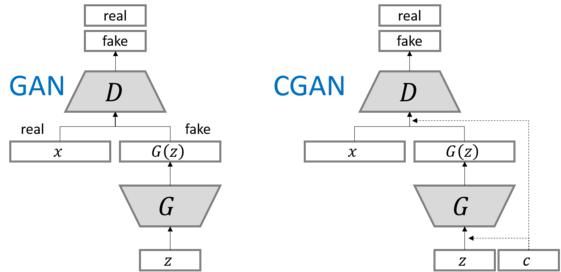
CausalGAN introduces a causal implicit generative model (CiGM) that can sample from a conditional and interventional distribution of labels. CausalGAN treats the presence or absence of a label as an intervention: do(Mustache = 1). Typically with Conditional GAN, the labels are independent of each other where choosing one label does not affect the distribution of other. Kocaoglu, et al. point out that generating an image conditioned on labels is actually a causal process. For example, gender causes mustache: \(G \rightarrow M\). Labels end up determining the image distribution and a causal graph can be constructed between the gender and mustache labels. Intervening on a label fixes the value of the variable, such as \(Mustache = 1\), without effecting its ancestors, only effecting its descendants. This is different than conditioning which they assert is like using an empty set of graphs. For example, by intervening on \(Gender = Female\), will then cause all its descendants to have mustaches.

An important distinction of the CausalGAN paper is that it does not learn the underlying graph (neither does CGM). It uses a Bayesian network and assumes the causal graph is given.
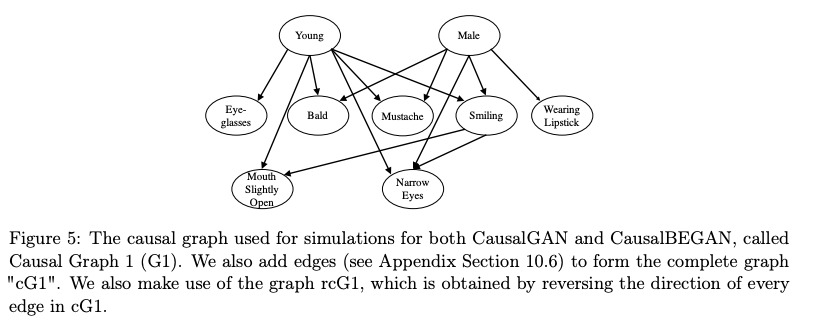
Hence, later we will see that you have to define a causal graph in order to use CausalGAN. Rather, this paper focuses on learning a causal model - all the functions and distributions of exogenous variables acting on the causal structural model:
\[M = (V, E, F, P_E(\dot)))\]
where M is the causal model, V is a set of random observable variables, E is exogenous (confounding, unobservable) variables, F is a set of functions, \(P_E\) is the probability distribution over E, and D is a causal graph over V. A key principle of this paper is leveraging the universal approximation of neural networks.
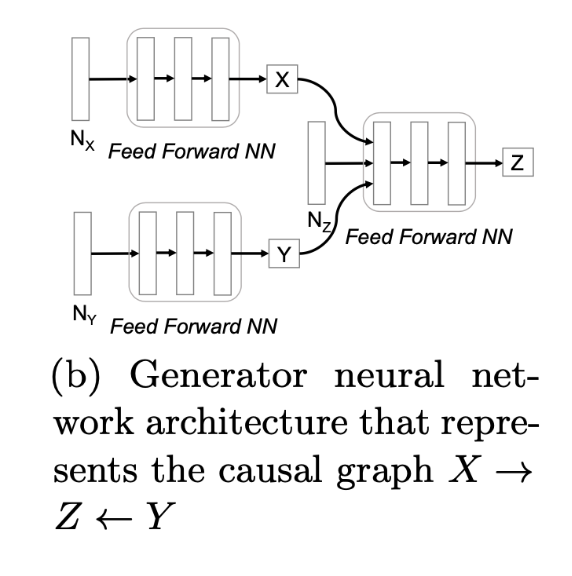
For example, a causal graph can be represented as:
\[X = f_x(N_x)\]
\[Y = f_y(N_y)\]
\[Z = f_z(N_z)\]
Feed-forward networks represent \(f_x, f_y, f_z\) and random Gaussian noise represents \(N_x, N_y, N_z\) which have to be jointly independent. In the CausalGAN approach, you need to start by defining a causal graph. CausalGAN is a 2-Step process and the architecture is shown below: 1) Train a model over the labels with Wasserstein GAN (WGAN) acting as a Causal Controller and 2) Train a generative model over the images conditioned on the labels, by using CausalGAN.
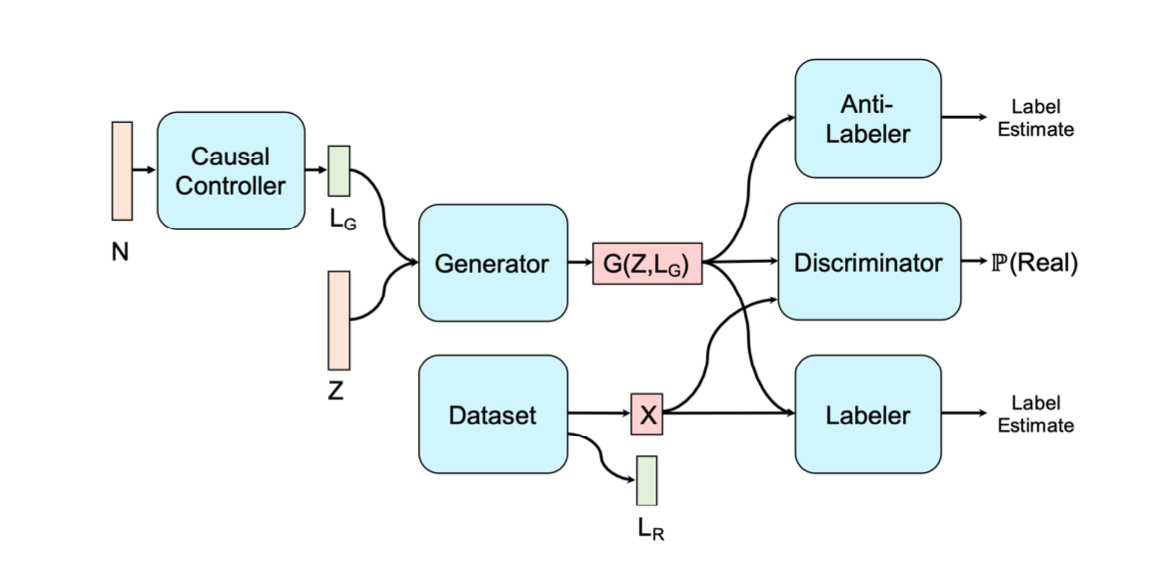
The Causal Controller is responsible for sequentially outputting discrete labels, which is performed by WGAN. Normally, for challenges such as image captioning when using GAN, the generator's gradients must be treated with a reinforcement learning policy since the maximum likelihood of the GAN objective does not allow for non-continuous outputs. However, using WGAN is a way to bypass this approach. CausalGAN is the CiGM that models the label-conditional image generation, and passes is output, \(G(Z, L_G)\)to two neural networks - a Labeler and an Anti-Labeler. The Labeler estimates the labels from the images in the true data distribution, and the Anti-Labeler estimates the labels from the images in the generated distribution. The goal of the Generator, implemented as a Deep-Convolutional GAN (DCGAN) , is to: 1) make realistic images, 2) minimize the Labeler Loss (i.e. make realistic images conditioned on labels, 3) maximize the Anti-Labeler Loss (i.e. make it difficult for poor images to be generated and labeled as such).
Counterfactual Generative Networks (CGN)
An image classifier trained on cows may have learned factors that are spuriously correlated with the image - green pastures, for example. But if presented a purple cow on a sky background, the classifier will fail. In order to train a robust, invariant image classifier, Sauer and Geiger generates counterfactual images by asking: "How would this image look like with a different background?"

Their approach is a novel generative model that enables full control over several factors that are relevant for image classification. Their aim is to generate counterfactual images with previously unseen combinations like a red wine glass with the texture of carbonara pasta and a baseball field background shown above. Sauer and Geiger disentangle spurious correlations from causal relationships across objects in ImageNet and MNIST. They use causal concepts similar to CausalGAN, through the use of independent mechanisms (IM) that are defined as causal processes that occur autonomously and independently of one another, and do not influence each other. They apply interventional treatments on specific IMs where each one controls a factor of the object specifically three - 1) shape, 2) background, and 3) texture. Like CausalGAN, they argue that factors like shape, texture, and background are assumed to be statistically independent. But in reality, these factors are often times correlated in the training data but some combinations (like purple cow on sky background) do not exist. Although a VAE has been used for disentanglement, VAEs cannot generate new combinations of images if none of these samples are in the original training set.
As a result, by disentangling these factors, and controlling each of them, they show that the CGN that can generate counterfactual images - images of unseen combinations of factors not in the training dataset. They then use these counterfactual images to train a robust, invariant image classifier. Their approach links the fields of disentangled generative models and robust classification. Instead of training a huge network to automatically map from some low-dimensional to high-dimensional space, they break up the CGN into smaller networks as shown below.
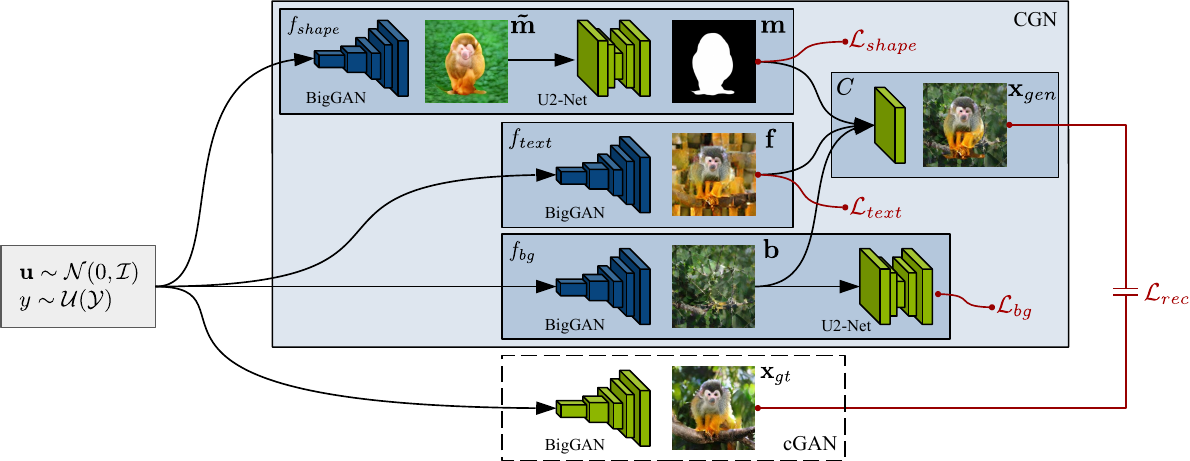
Each network, like the CausalGAN idea, is a separate function which are each autonomous. Autonomous means the ability to change one factor (like background), while keeping all other factors fixed (don't change shape and texture). They propose a structural causal model, SCM:
\[S_j \coloneqq {f_j(PA_j, U_j)}\]
where each random variable \(S_j\) is a function of its parents \(PA_j \in {S_1, ..., S_d} \mathbin{/} {S_j}\) and noise variable \(U_j\) where the noise variables \(U_1, ... U_d\) are jointly independent.
For example, the SCM for MNIST is:
\[M \coloneqq {f_{shape}(Y_1, U_1)}\]
\(F \coloneqq {f_{text, 1}(Y_2, U_2)}\), \(B \coloneqq {f_{text, 2}(Y_3, U_3)}\), \(X_{gen} \coloneqq {C(M, F,B)}\) where as we see later C is a network (function) for composing the image. The functions \(f_j\) are IMs, where intervening on one function does not change the other functions \({Sf_1, ..., f_d} \mathbin{/} {f_j}\). Each IM (function) is conditioned on a different class label, \(a\). The intervention is defined as \(S_k \coloneqq \tilde{f}(PA_k, \tilde{U_k})\) where \(P_S^{do(S_k \coloneqq a)}\). The interventional images are \(X_{IV}\)that are taken from the intervention distribution \(P_S^{do(S_k \coloneqq a)}\). To generate the counterfactual images \(X_{CF}\), they fix the noise and randomly draw \(a\). They then train an invariant classifier, \(r: X_{CF} \rightarrow Y_{C,F,k}\) on real and counterfactual images to predict the label that was provided to one specific IM.
Like CausalGAN, they assume the causal structure is already known and focus on learning three IMs, shown in the CGN architecture. As they mentioned, each function is broken down into smaller parts. As a result there is a separate BigGAN for \(f_{shape}, f_{texture}, f_{background}\). Instead of using an adversarial loss, they train a conditional GAN to generate a stronger signal by outputting a pseudo-realistic \(x_{gt}\). They use a combination of L1 and perceptual loss as a total reconstruction loss to compare it to what the \(C\) composite network outputs, which is \(x_{gen}\). Each function has its own loss, as well \(L_{shape}, L_{texture}, L_{background}\).
Github repos:
CausalGAN - https://github.com/mkocaoglu/CausalGAN (Tensorflow)
Counterfactual GANs - https://github.com/autonomousvision/counterfactual_generative_networks(PyTorch)
Additional papers:
DeepSCM https://arxiv.org/abs/2006.06485
Visual Commonsense R-CNN https://arxiv.org/abs/2002.12204
Recommended Reading:
http://bayes.cs.ucla.edu/jp_home.html