"How transferable are features in deep neural networks"

A paper review of Yosinski, Jason, et al. "How transferable are features in deep neural networks?." Advances in neural information processing systems. 2014.

Slides available here.

Summary

Drawing on the recent work in 2014 of transfer learning, Yosinski et al. explore the transition between general and specific layers. They investigate three primary research questions in the paper:

1. Can we quantify the degree to which a particular layer is general or specific?
2. Does the transition occur suddenly at a single layer, or is it spread out over several layers?
3. Where does this transition take place: near the first, middle, or last layer of the network?

To this extent, they run several experiments comparing the performance of eight different transfer learning experiments against a trained 8-layer convolutional neural network on approximately 645,000 images depicting 500 classes from ImageNet.  They find that the use fine tuning a target network with gradients learned across the transferred weights from the base network, can boost generalization no matter which layer.  They assert that the effect of generalization lingers improving performance over random initialization, alone. Further, they introduce the concept of co-adaptation where middle layers of a CNN suffers from fragile co-adaptation, but later layers in the network do not where optimization is easy to recover features.

AlexNet and Visualization of Weights

Krizehevsky et al. introduced the famous AlexNet in 2017  that included weights learned by the first convolutional layer on an input 224 x 224 image. This visualization of the weights across 96 convolutional kernels of size 11 x 11 x 3 depicts Gabor-like filters which Yosinski refers to as standard fare in the illustration of weights in CNNs. Gabor filters as we know, is a linear filter used for texture analysis and through signal processing shows the frequency content of an image. Orientation, rotation, and different factors are parameters that visualize the texture representation. Some have even found that Gabor filters are similar to those of the human visual system. Today seeing anything except for Gabor-like filters in learned weights is unusual, leading to suspected bugs in code or signaling problems in the CNN training process.

It is these Gabor-like filters that Yosinki et al. ponder about – how general are they in one layer, versus another? They seek to explore and characterize the transition from general learned features as viewed by the activation maps, from the bottom layers, to the top-most layers that are closest to the classifier which are more specific for the target task. Zeiler et al.  also investigated this effect through an 8-layer CNN similar to AlexNet. They visualized the feature maps across each layer and found that features in the top layers are more specific to the chosen dataset task, with more specific features, less abstract than those at the bottom near the input.

Yosinksi et al. appear to continue on this thread and take an 8-layer CNN to dissect three questions:

1. Can we quantify the degree to which a particular layer is general or specific?
2. Does the transition occur suddenly at a single layer, or is it spread out over several layers?
3. Where does this transition take place: near the first, middle, or last layer of the network?

Transfer Learning

With transfer learning, they structure their experiments across two primary techniques which are fine-tuning and freezing. With fine-tuning, the network is allowed to backpropogate errors from the target to base network and finetune the base network to the new task. With freezing, the transferred layers from the base network are frozen meaning that they are not updated during backpropogation. Only the base network features are used. In this case, they can initialize on pretrained weights instead of random initialization, such as the “base B” network they later refer to. In practice, we can use ImageNet as pretrained weights. For freezing, we can use the pretrained network as a feature extractor. Freeze the entire convolutional layers, and do not update weights on the last fully connected layer, as an example. That last layer is just randomly initialized weights. These two concepts are important to keep in mind as Yosinski builds his experiments using fine-tuned and frozen networks.

Key Contributions

The paper’s key contributions are to quantify the degree to which a particular layer is general or specific. It answers how well features at that specific layer transfer from one task to another. Their primary conclusions were the following:

1. Two issues occur that degrade performance when using transferred features without fine-tuning: a) how specific the features are, b) optimization difficulties between co-adapted neurons.
2. Quantify how performance declines when the base and target become increasingly dissimilar.
3. Find that transferred weights perform better than random weights, even on smaller datasets.
4. Initializing a network from any number of layers (the 1st, the first 2, the first n) boosts generalization performance and the effects of having seen the first dataset (e.g. ImageNet) persists even after a lot of fine tuning.

Experimental Design

Their experimental design involved the training of two tasks – A and B. Each is a 500-class multi-class CNN. ImageNet was the dataset used and was randomly split into two approximately even groups of 500 classes, 645,000 images, and non-overlapping subsets. Regarding subsets, ImageNet contains clusters of similar classes, particularly dogs and cats, like these 13 classes from the biological family Felidae: {tabby cat, tiger cat, Persian cat, Siamese cat, Egyptian cat, mountain lion, lynx, leopard, snow leopard, jaguar, lion, tiger, cheetah}.

On average, A and B will each contain approximately 6 or 7 of these felid classes, meaning that base networks trained on each dataset will have features at all levels that help classify some types of felids. An 8-layer CNN was trained on Tasks A and B where baseA network has more man-made entity images and baseB network has more natural entities. The experimental transfer learning networks are the following: a control called “selffer” and a “transfer” network.  Consider for example, the “selffer” network which would include the first 3 layers copied from baseB, then frozen. The remaining layers 4 - 8 are initialized randomly and trained on dataset B. B3B+ is fine-tuned, allowing layers 4 - 8 to learn. Next let’s consider the “Transfer” network. Take for example, the first 3 layers copied from baseA and frozen. Layers 4 - 8 are initialized randomly as well, and trained on dataset B.  The authors hypothesize that if A3B performance == baseB performance, then the 3rd layer has generalization properties. But if A3B performance < baseB performance, 3rd layer properties are specific to A not B. They repeated these experiments for n in {1, 2, … 7} and in both directions AnB, BnA, like the following examples: B1B-/+, B2B-/+, B3B-/+ … B7B-/+, A1B-+ …, B7A-/+ (where + means fine-tune and – means frozen).

Empirical Results

The base case is to compare all experiments against baseB. The top accuracy was 0.625. We can see that in Figure 2 there is interesting middle-layer behavior occurring. Consider layers 1 to 4 are frozen from B data. Layers 5 – 8 are randomly initialized. Similarly, layers 1 to 5 are frozen from B data, and layers 6 – 8 are randomly initialized. They discover that performance drops when they transfer up to layers 4 and 5 because there exists fragile co-adaptation. These are features that interact with each other in complex ways, so complex that they can’t be relearned in upper layers. There is less co-adaptation between layers 6-7 and 7-8, and more in the middle layers. We might also think about this in a different way as pointed out by the authors, that relearning the last two layers as the networks gets closer to the softmax layer isn’t too hard for the optimizer! When turning our attention to the fine-tuning self BnB+, they show that fine-tuning prevents the performance drop observed in selfer BnB - allowing the later layers to relearn and update gradients is equivalent performance to the base case. But the worst performance occurs with transfer AnB. In the AnB experiments, particularly layers 4 - 7 show significant drop in performance, meaning that two things are happening according to Yoskin et al: 1) They lost co-adaptation as shown earlier, and 2) The drop is happening when there are fewer and fewer features to train on.

But their most important results come from empirically demonstrating how transfer AnB+ performs. Transferring features and then fine-tuning them results in networks that generalize better than those trained directly on the target dataset. They find that transferring with fine-tuning boosts performance no matter which layer, compared to baseB accuracy. This occurs even after 450,000 training iterations, still boosting generalization meaning that the effects of seeing the baseA features still lingers. In addition, generalization improvement occurs no matter which layer the transfer learning occurs.

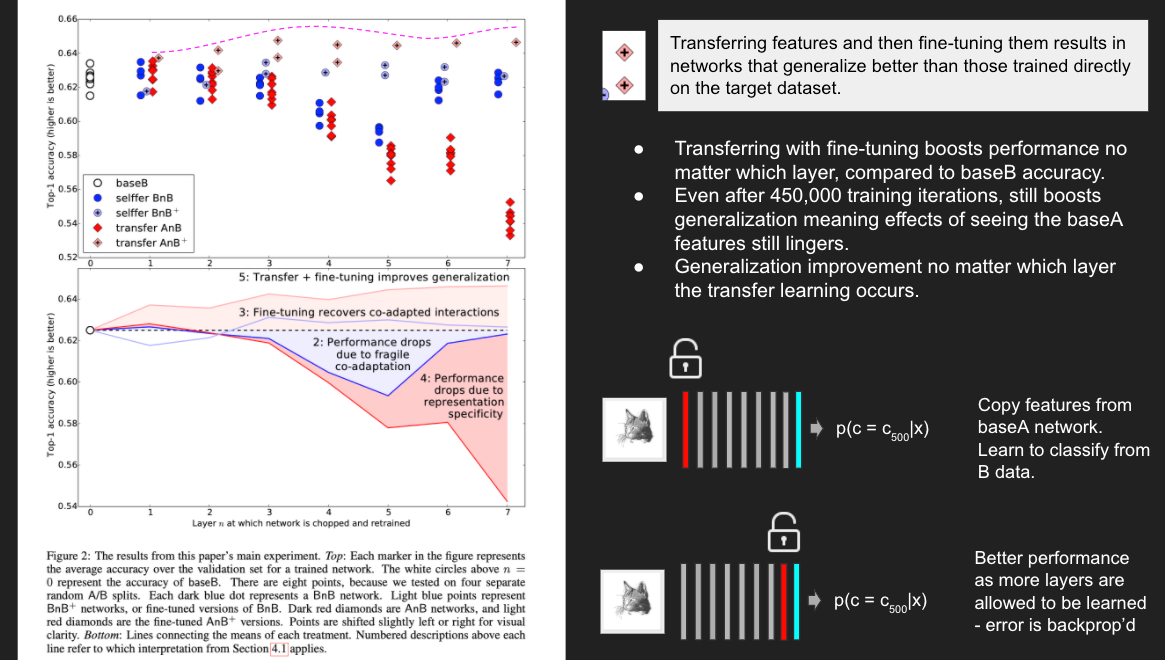
Lastly, they show brief results of their earlier assertion about similarity between task A and task B datasets. In Figure 3 they compare how transferring weights improves performance compared to other studies of the day that asserted how random, untrained weights would improve performance equally. We can see in Figure 3 that performance falls off quickly at layer 2. They also show that when BnA copies baseB (natural) features to train A (man-made images), the accuracy is declines and they somehow intimate that this direction implies challenges in feature learning.  But their plots are intended to show that the network is trained on transferred weights across more and more layers, the final 8 - n layers become increasingly dissimilar and performance declines.  They also try to show that transferring even from a distant task is better than using random filters.

Pros:

• Overall very easy to read, as this is an empirical applications paper as opposed to mathematical.
• Co-adaptation occurs in upper layers more than downstream layers; Showing that optimization may be worse in the middle. Would have been interesting to have seen this more empirically tested.
• Empirically evaluated some assertions at the time by Jarett that showed random weights perform just as well on untrained, although it was done on 2 - 3 layers.

Cons:

• They note they went in both directions, but the Figure 2 seems to only communicate AnB; what about BnA? For example, is Figure 2 transfer AnB+ also the same as BnA+? Wouldn’t we expect to see similar performance gains regardless of man-made or natural entities, since both datasets are fairly similar? I’m not very convinced about their assessment of dissimilarity, as well.
• Loose assertion implicitly made in Section 2 about how the degree of generality of a set of features learned on task A and its usability on task B, is somehow dependent on similarity between A and B, yet no quantification of similarity was conducted. Except for splitting A and B data into two semantically different sets.
• They indicate “lingering effects” of generalization improvement. How would one quantify or prove “lingering”?

References:

[1] Krizhevsky, Alex, Ilya Sutskever, and Geoffrey E. Hinton. "Imagenet classification with deep convolutional neural networks." Communications of the ACM 60.6 (2017): 84-90.

[2] Zeiler, Matthew D., and Rob Fergus. "Visualizing and understanding convolutional networks." European conference on computer vision. Springer, Cham, 2014.