Off my machine learning bucket list - the MNIST Tensorflow Tutorial

I'm definitely no where close to a deep learning expert. But, I'm pretty curious and interested to learn more about it and how I could start using it for "everyday" business problems. Decided to get started this morning and delve into the first TensorFlow tutorial on MNIST.
Basically I watched this guy's video on YouTube and his explanation of deep learning (Google Cloud Next 17). The guy is probably some super senior executive Google guy. Anyway, at around 30:20 he talks about doing this on TensorFlow with the MNIST digits database, so decided to give it a whirl.

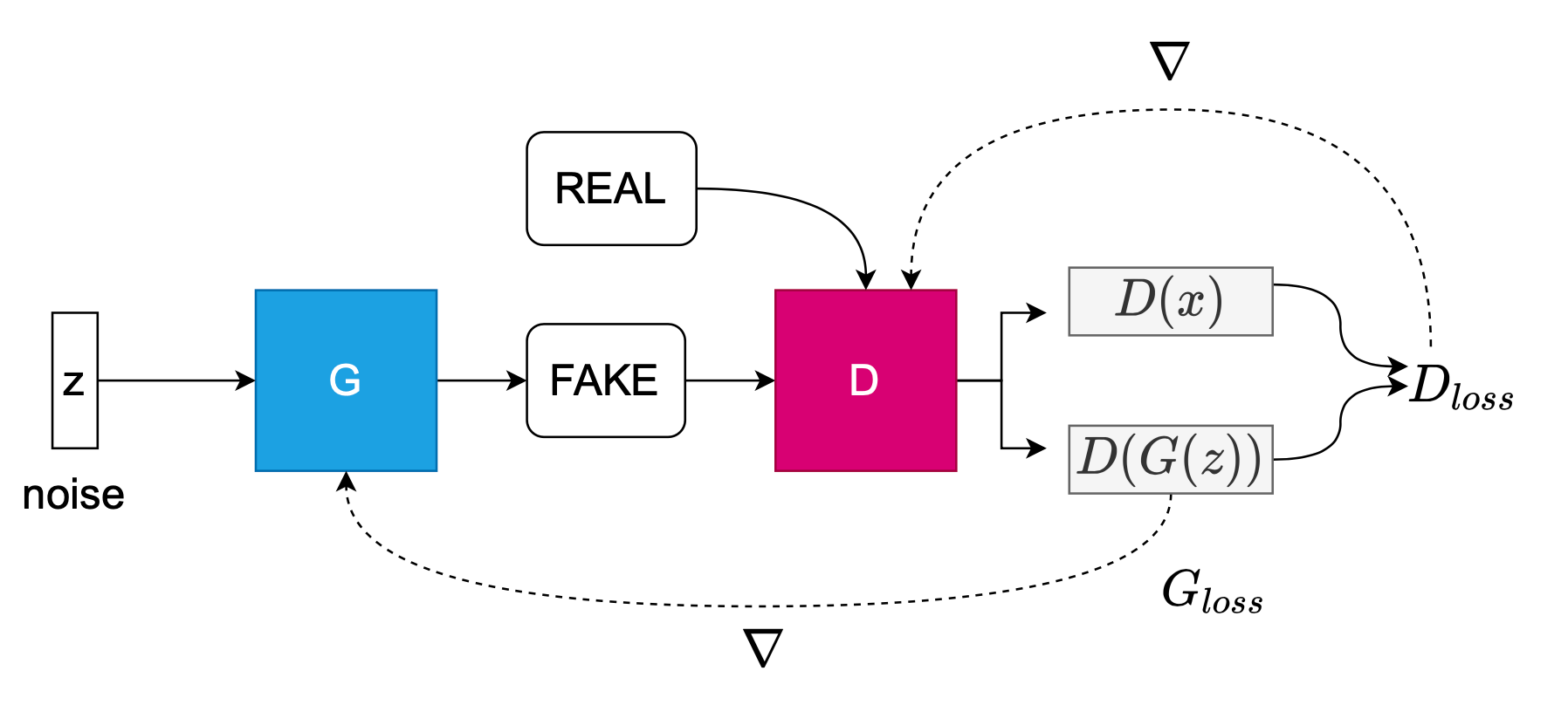
Image: Ref: https://www.slideshare.net/enakai/your-first-tensorflow-programming-with-jupyter, Etsuji Nakai Google
I've provided my script at the end of this post, which you could just copy and paste to run in your IDE. It's the exact same verbatim as the TensorFlow MNIST tutorial: https://www.tensorflow.org/get_started/mnist/beginners. However, it helped me to document the hell out of it going line by line through the tutorial until I really understand what was happening. It helps to chronicle what each line means in order for me to understand each step in the process.
What I learned from the MNIST tutorial for TensorFlow is that it's very important to really understand the basic and pretty straight-forward formula for softmax regression. After understanding that, and plugging it in as two initialized tensors (the weight and the bias) which are the variables in TensorFlow, you move on to another important formula for cross-entropy, essentially measuring the loss of the model. Once cross-entropy is defined, you're ready to train your model.

Check out this video here, Neural Networks Demystified. Softmax explanation starting at 0:11. (This is like one of the prettiest data science videos I've ever seen, btw.) https://www.youtube.com/watch?v=GlcnxUlrtek
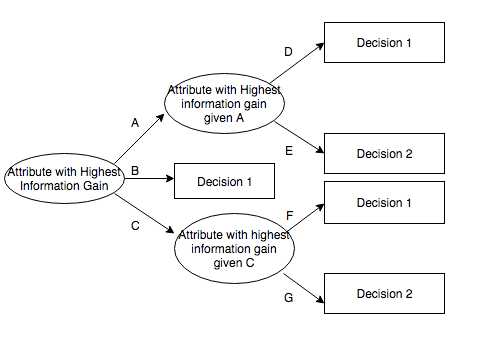
Image: https://www.slideshare.net/abhishekvijayvargia/decision-tree-softmax-regression-and-ensemble-methods-in-machine-learning, Abhishek Vijayvargia
I thought the coolest part of Tensorflow was this very statement, "it can automatically use the backpropagation algorithm to efficiently determine how your variables affect the loss you ask it to minimize. Then it can apply your choice of optimization algorithm to modify the variables and reduce the loss."
I thought this was neat because 1) it may prevent a lot of back and forth hyperparameter optimization experimentation, 2) it may assist in maximizing the features you've already engineered, and 3) being able to select your optimization algorithm (this tutorial they use a gradient optimizer), which may help select the right model right off the bat, after some experience, as opposed to what I've been accustomed to learning using sklearn's estimator chart.
Check out this blog from Illia Polosukhin using sklearn and TensorFlow together on the Titanic Dataset,"Note, that because of the fully differentiable nature of the TensorFlow components (and other Deep Learning frameworks), this allows to “train” the most optimal representation for your task. This has shown been the most powerful tool in the Deep Learning toolkit as it removes need to do manual feature engineering."
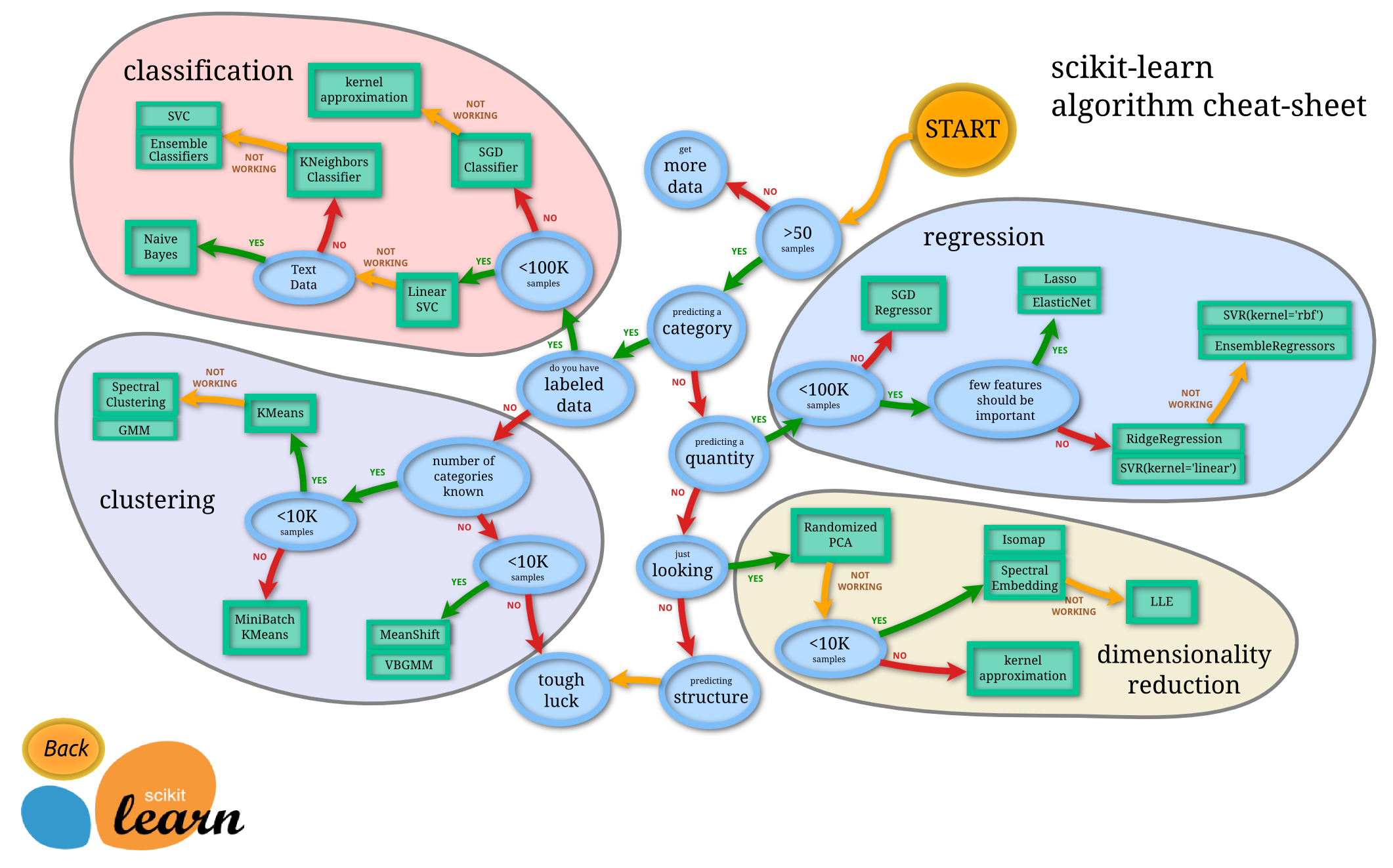
At the end of TensorFlow's tutorial, the softmax model results in 92% accuracy which isn't very good, per the tutorial. This page linked from TensorFlow provides the current leaderboard for the "Who is the best in MNIST, CIFAR-10, etc." and links to a variety of papers in the field.
Enjoy and send me your thoughts about your voyages with TensorFlow. Next thing, Keras.
"""In this tutorial, we're going to train a model to look at images and predict what digits they are. MNIST number recognition regression problem using softmax. predict y is a digit from 0 - 10. """
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
""" Onehot encode to turn the digit features 1- 10 as dummy data variables. x isn't a specific value. It's a placeholder, a value that we'll input when we ask TensorFlow to run a computation. We want to be able to input any number of MNIST images, each flattened into a 784-dimensional vector. We represent this as a 2-D tensor of floating-point numbers, with a shape [None, 784]. (Here None means that a dimension can be of any length.)
Each image is 28 pixels by 28 pixels. We can interpret this as a big array of numbers: We can flatten this array into a vector of 28x28 = 784 numbers. 784 dimensional vector space """
x = tf.placeholder(tf.float32, [None, 784])
""" Need the weights and biases: A Variable is a modifiable tensor that lives in TensorFlow's graph of interacting operations. It can be used and even modified by the computation. For machine learning applications, one generally has the model parameters be Variables.
y = softmax(Wx + b)
yn = softmax[wn * xn + bn] (several n times over)"""
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
"""we initialize both W and b as tensors full of zeros. Since we are going to learn W and b, it doesn't matter very much what they initially are."""
#implement the model
"""First, we multiply x by W with the expression tf.matmul(x, W). This is flipped from when we multiplied them in our equation, where we had Wx, as a small trick to deal with x being a 2D tensor with multiple inputs. We then add b, and finally apply tf.nn.softmax."""
y = tf.nn.softmax(tf.matmul(x, W) + b)
#Train
""" To measure model loss we use cross-entropy:
Hy'(y) = -Sigma (y'i) * log(yi)
where y': True Value
and y: Predicted Value (one of the one-hot-encoded digits). To implement cross-entropy we need to first add a new placeholder to input the correct answers."""
y_ = tf.placeholder(tf.float32, [None, 10])
#Then we can implement the cross-entropy function
""" First, tf.log computes the logarithm of each element of y. Next, we multiply each element of y_ with the corresponding element of tf.log(y). Then tf.reduce_sum adds the elements in the second dimension of y, due to the reduction_indices=[1] parameter. Finally, tf.reduce_mean computes the mean over all the examples in the batch. See commented model loss formula above: """
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))
""" Now that we know what we want our model to do, it's very easy to have TensorFlow train it to do so. Because TensorFlow knows the entire graph of your computations, it can automatically use the backpropagation algorithm to efficiently determine how your variables affect the loss you ask it to minimize. Then it can apply your choice of optimization algorithm to modify the variables and reduce the loss.
In this case, we ask TensorFlow to minimize cross_entropy using the gradient descent algorithm with a learning rate of 0.5. Gradient descent is a simple procedure, where TensorFlow simply shifts each variable a little bit in the direction that reduces the cost. But TensorFlow also provides many other optimization algorithms: using one is as simple as tweaking one line. List of other optimizers: https://www.tensorflow.org/api_guides/python/train#optimizers"""
#train with gradient descent optimizer
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
"""We can now launch the model in an InteractiveSession:"""
sess = tf.InteractiveSession()
#Let's train -- we'll run the training step 1000 times!
#We first have to create an operation to initialize the variables we created:
tf.global_variables_initializer().run()
"""Each step of the loop, we get a "batch" of one hundred random data points from our training set. We run train_step feeding in the batches data to replace the placeholders. Using small batches of random data is called stochastic training -- in this case, stochastic gradient descent. """
for _ in range(1000):
batch_xs, batch_ys = mnist.train.next_batch(100)
sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
#Evaluation
"""Well, first let's figure out where we predicted the correct label.
tf.argmax is an extremely useful function which gives you the index of the highest entry in a tensor along some axis. For example, tf.argmax(y,1) is the label our model thinks is most likely for each input, while tf.argmax(y_,1) is the correct label.
We can use tf.equal to check if our prediction matches the truth."""
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
"""That gives us a list of booleans. To determine what fraction are correct, we cast to floating point numbers and then take the mean. For example, [True, False, True, True] would become [1,0,1,1] which would become 0.75."""
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
"""Finally, we ask for our accuracy on our test data."""
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))
"""92% accuracy which isn't very good, per Google. List of other methods to use for this MNIST problem, here: http://rodrigob.github.io/are_we_there_yet/build/classification_datasets_results.html"""